# Rasterization

光栅化 就是将获得的图像在显示器件上成像的过程，Raster 在德语里是屏幕的意思，所以光栅化也就是在屏幕成像绘制的意思。所以我们需要了解一些屏幕成像的概念，原理和方法。

# Basic Concept

Pixel (short for “picture element”) 像素

一个有着统一颜色的平方单位
这个颜色由三种颜色混合而来（RGB）

Resolution 分辨率：表示像素的规模

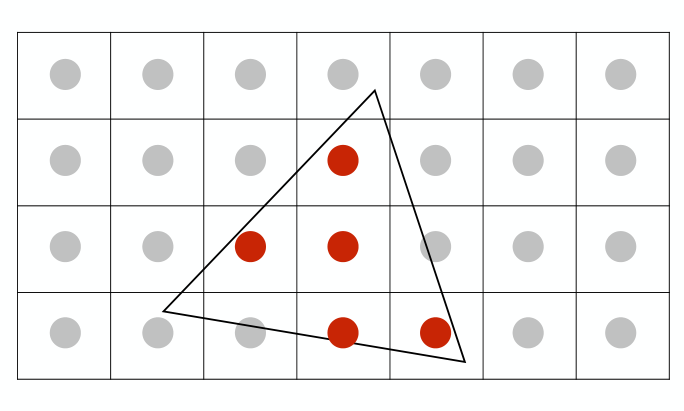
Screen Space：屏幕空间用于准确描述屏幕具体像素的工具

像素的描述点 $(x,y)$ ，其中 x 和 y 均为整数
像素点的范围从 $(0,0) \to (width -1,height-1)$
像素点的中心在 $(x + 0.5,y+0.5)$
屏幕的覆盖范围 $(0,0) \to (width,height)$

三角形网络：以三角形为基础元素构成的多变形 Triangle Meshes

三角形作为简单的多边形由以下的优点：

能够保证是平面，一个三角形就是一个平面
有明确的内部定义
有明确的方法对顶点和重心进行插值

# Sampling

我们获得目标图像后，需要通过采样的方式来获得最终那些像素需要变成什么颜色，在三角形中我们判断像素的重点是否在三角形的内部，如果是就是需要设置的点，如果不是就不需要。

根据这个我们就能写出一个基本的函数关系：

$inside(t,x,y) = \left\{ \begin{array}{c} 1 \space in \\ 0 \space out \end{array} \right.$

Note：这个信号领域的冲激函数非常像

有了基本的模型我们就能写出伪代码：

for (int x = 0; x < xmax; ++x)
    for (int y = 0; y < ymax; ++y)
        image[x][y] = inside(tri,x + 0.5,y + 0.5);

在 inside() 这个函数中，我们需要传入一个目标三角形，还有需要确认的像素点的坐标，判断点是否在三角形内。这里的判断就用到了之前提到的向量叉乘，

同时为了简化判断范围，我们只需考虑三角形顶点的 $x_{min} \to x_{max}$ 的范围和y_{min} \to y_

通过采样出来的图像显示出来为：

很显然，出来的效果和原图像有一定的差异，存在明显的锯齿（Jaggies）

# Antialiasing

因为现在图像均是通过采样后在输出来实现对图像的模拟，所有会存在不同程度的问题，我们称之为 Artifacts（瑕疵），而 Artifacts 的出现主要是因为采样出现了 Aliasing “混叠”，混叠包括空间上和时间上的，两种情况都会导致图像出现异常，而解决的方法就是了解 Aliasing 出现的原因。

采样在空间上出现采样率过低体现为：锯齿
采样的空间频率没有远低于图像的空间频率：摩尔纹
采样在时间上出现采样率过低体现为：车轮效应

# Background Knowledge

在信号学领域，有两个非常重要的概念一个叫时域，一个叫频域。时域是以时间为自变量的描述，频域是以频率为自变量的描述。

这里要引入傅里叶变换，三角函数来组合复杂的周期函数，这些都基于三角函数的基本变化规律，如下图。

$f(t) = A_0 + \sum_{n=1}^\infty A_n \sin(nwt + \varphi_n)$

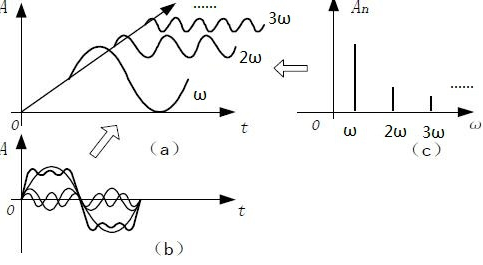
有了这些基本的概念后，我们再把这些知识和图像采样联系起来，我们的在做图像采样的时候，就好像对一个函数进行离散取值，然后通过值去还原这个函数。

如果我采样的频率不够高，就会出现采样的点还原出来的函数有问题，图像有问题，如下图所示。

在采样率一样的情况下，高频信号的波形完全丢失，用低频信号的频率采集的值最终和低频的信息加起来的结果就是错误的。为了保证采样的正确性，我们需要遵守奈奎斯特–香农采样定理：为了不失真地恢复模拟信号，采样频率应该不小于模拟信号频谱中最高频率的 2 倍。

# Filter

了解基本的知识背景后，我们来看图像的信息。一张图像是由一个像素矩阵构成的，现在我们把像素矩阵进行调整，只保留一行，其他行接到第一行的后面。这样我们就能把像素矩阵变成一个数组的结构，而数组的每一个值就是对应像素在图像上的值（RGB），这样我们就能把这个图像变成一个函数，既然是一个函数，我们就能够通过傅里叶级数把他转换成各种基本的周期函数的加和。同样的我们就能够对转换后的这个函数进行变换，使得时域的函数转化为频域的函数，如下图就是转化后的